Tipos de Gráficas
Gráficas Circulares:
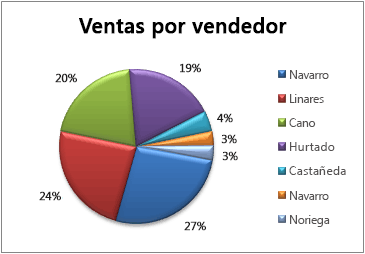
Denominadas también gráficas de pastel o gráficas del 100%, se utilizan para mostrar porcentajes y proporciones, estas gráficas nos permitan ver la distribución interna de los datos que representan un hecho, en forma de porcentajes, sobre un total.
 Gráficas de Barras:
Gráficas de Barras:
Se emplea para ilustrar muestras agrupadas en intervalos. Está formada por rectángulos unidos a otros, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados. En el eje vertical se representa la frecuencias, y en eje horizontal los valores de las variables. La altura de cada rectángulo es proporcional a la frecuencia del intervalo respectivo.
Gráficas de Líneas:
Muestra la relación entre dos variables cuantitativas. En este tipo de gráfico se representa los valores en dos ejes cartesianos. Las gráficas lineales se recomienda para presentar series en el tiempo y es donde se muestra valores máximos y mínimos; también se utiliza para varias muestras en un diagrama.
Pictograma:
Es un diagrama que utiliza imágenes o símbolos para mostrar datos para rápida visualización y compresión. En un pictograma se utiliza una imagen o símbolo para representar una cantidad específica.
Gráficas Radiales:
Las gráficas radiales comparan los valores agregados de varias series de datos y muestra cambio de valores con relación a un punto central.
Bibliografía: Libro de Estrategia de Razonamiento(Ejercicios - Séptima Edición)
Autores del libro : Mgtr. Jorge Estuardo Sánchez Fuentes y Ing. César Leonel Ovalle Rodríguez.


































